[비대칭키 알고리즘] DH, RSA의 수학적 자물쇠와 그 취약점 보완

들어가며

 HTTPS의 주요 기술인 '키 교환'과 '디지털 서명'은 '비대칭키' 알고리즘을 사용합니다. 비대칭키는 '개인키'-'공개키' 쌍으로 이루어진 키를 말하는데, 공개키는 말 그대로 누구에게나 공개되는 반면, 개인키는 비밀로 유지되어야 합니다. 이 글에서는 키 교환과 디지털 서명의 대표적인 알고리즘인 DH(Diffie-Hellman)와 RSA(Riveset-Shamir-Adelman)를 다룹니다.

 

 비대칭키 방식의 DH와 RSA는 정방향으로 계산하기 쉽지만 역방향 계산은 어려운 '일방향 함수'의 개념을 활용합니다. 예를 들어, 큰 두 수의 곱셈은 쉽지만 큰 합성수에 대한 소인수 분해는 어렵습니다. 이와 같이 DH로 생성된 대칭키를 유추하거나, RSA로 암호화된 데이터를 복호화하려면 매우 어려운 역 연산을 수행해야 합니다.

 

 일방향 함수의 역 연산이 어렵다는 특성은 '수학적 자물쇠'에 비유되곤 합니다. 단, 이 자물쇠는 수학으로 만들어졌기 때문에 니퍼로 따는 등의 편법은 사용할 수 없습니다.. 수학적 자물쇠, 정말 찰떡같은 비유 아닌가요?!🤓 하지만 이 완벽해보이는 자물쇠에도 취약점이 존재합니다. 힌트는 해당 자물쇠를 푼다는 패러다임에서 벗어나는 것입니다. 더 자세한 힌트는 아래 목차에 나와있습니다. 그럼 DH와 RSA가 각각 어떤 수학적 자물쇠를 사용하는지, 그 원리와 취약점을 분석하러 함께 가보시죠!

 

 

목차

1. 모듈로 연산

2. DH(Diffie-Hellman)

3. RSA(Rivest-Shamir-Adelman)

4. 자물쇠를 새로 만들어버린다면 어쩔건데?

5. 마무리

6. Reference

 

---

 

1. 모듈로 연산

 모듈로 연산은 DH와 RSA가 사용하는 일방향 함수의 핵심 개념이며, 정수론 및 컴퓨터 보안 등 여러 분야에서 유용하게 사용되므로 간단하게 정리하고 지나가겠습니다. 2. DH부터 보시고 궁금한 부분이 생기면 다시 올라와서 보셔도 됩니다.

---

 모듈로 연산은 합동 관계를 바탕으로 두 수의 관계를 정의합니다. 그럼 '모듈로'와 '합동'이라는 개념을 알아봐야겠네요. A≡B (mod C)라는 수식이 있습니다. 이 수식의 의미는 'A와 B는 mod C에 대해 합동이다' 입니다. 우선 mod는 모듈로(modular)의 약자로 '나머지 연산'을 말하며 '%' 연산자와 동일한 역할입니다. A mod C = R일 때, A는 피제수(나눠지는 수, devidend), C는 제수(나누는 수, devisor), R은 나머지(remainder)입니다. 또, '≡'이 의미하는 합동 연산자는 A mod C와 B mod C의 값이 같음을 나타냅니다. 한 번 더 풀어보면 A를 C로 나눈 나머지와 B를 C로 나눈 나머지가 같으므로 A와 B가 '동치류'라는 의미입니다. 

 

 동치류는 또 무엇일까요? figure1-1을 보시면 하나의 원판에 C개의 조각이 있습니다. 같은 조각 안에 있는 피제수들은 C라는 제수로 나눴을 때 합동이며, 같은 조각 안에 있는 피제수들을 동치류라고 합니다. 어떤 수를 C로 나눈 나머지는 언제나 0, 1, 2, ...C-2, C-1 중 하나이고, 그 어떤 수에 대한 모든 경우의 수는 반드시 저 원판 안에 속합니다. 그럼 정말 맞는지 함께 연산을 해봅시다!

 

 C에 3을 대입하고, C의 피제수를 0부터 1씩 증가시키면서 모듈로 연산을 해보겠습니다. 0을 3으로 나눈 나머지는 0, 1을 3으로 나눈 나머지는 1, 2를 3으로 나눈 나머지는 2, 3을 3으로 나눈 나머지는 다시 0, 4를 3으로 나눈 나머지는 다시 1입니다. 나머지가 0, 1, 2 안에서 반복되고 피제수 0, 3, 6, ...은 0의 조각, 1, 4, 7, ...는 1의 조각, 2, 5, 8, ...는 2의 조각에 들어갑니다. 즉, 0, 3, 6, ... 은 모두 3으로 나눈 나머지가 0이므로 mod 3에 대해 합동이며, 모두 0의 조각 안에 있으므로 동치류입니다. 1, 4, 7, ... 역시 mod 3에 대해서 합동인 동시에 1의 조각 안에 있는 동치류네요.

 

 이를 일반화해보면 0의 조각 안에는 C의 배수들, 1의 조각 안에는 C의 배수에 1을 더한 숫자들, 2의 조각 안에는 C의 배수에 2를 더한 숫자들, C-1의 조각 안에는 C의 배수에 C-1을 더한 숫자들이 동치류로서 존재합니다. 즉, A의 조각 안에 있는 숫자들은 모두 'A + C의 배수'로 나타낼 수 있으며, (A + C의 배수)와 A는 mod C에 대해서 합동입니다. C의 배수를 C로 나눈 나머지는 0이기 때문입니다. 이를 정리하면 임의의 정수 K에 대해서 (A + K·C) mod C = A mod C라는 식이 도출됩니다.

 

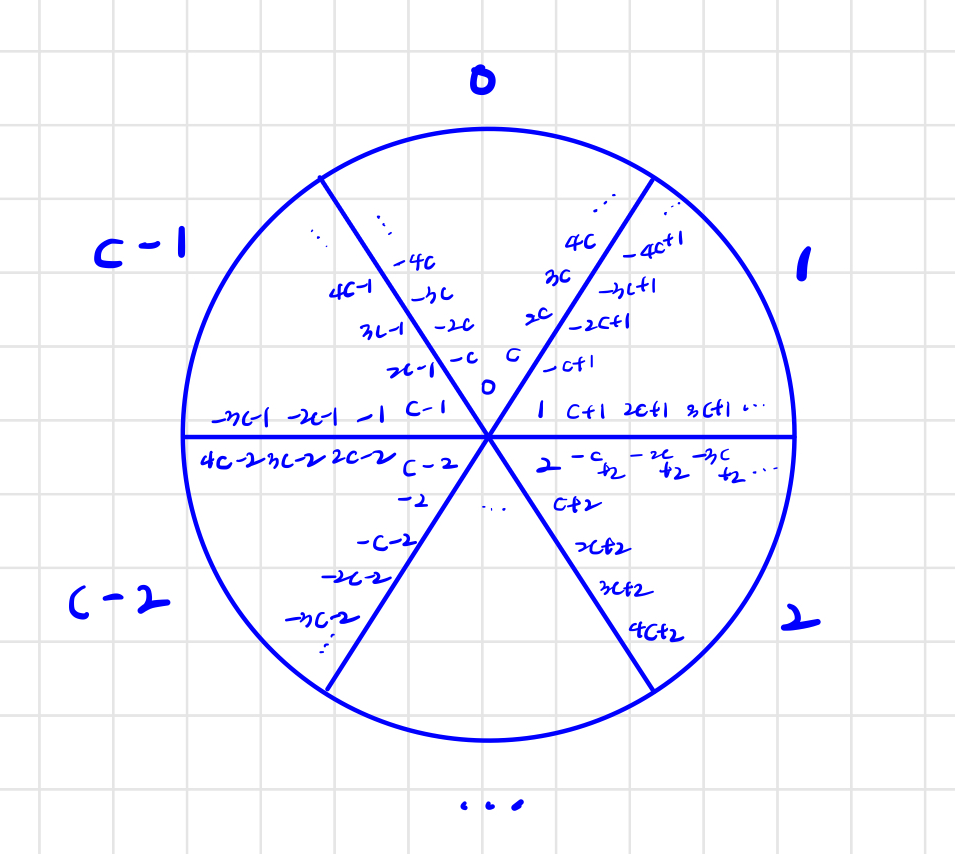
figure1-1. 모듈로 연산에서의 합동 관계

 아래 수식들은 DH와 RSA를 이해하는 데 필요한 모듈로 연산에 대한 정리입니다. 증명은 아래에서 덧셈에 대한 분배법칙만 해보고 나머지는 생략하겠습니다.  

모듈로 연산 분배 법칙
( A + B ) mod C =  ( A mod C + B mod C ) mod C
( A - B ) mod C =  ( A mod C  - B mod C ) mod C
( A × B ) mod C = ( A mod C × B mod C ) mod C

모듈로 연산 거듭제곱 법칙
( A ^ B ) mod C = (( A mod C ) ^ B ) mod C

모듈러 연산 결합법칙
(A mod C) mod C = A mod C

모듈로 연산 덧셈, 뺄셈, 곱셈 성질
A ≡ B (mod C)이고, E ≡ F (mod C)이면
A + E ≡ B + F (mod C), 
A - E ≡ B - F (mod C), 
A × E ≡ B × F (mod C) 이다.

모듈로 연산 제곱 성질 
A ≡ B (mod C)이면 A^K ≡ B^K (mod C)

모듈로 역수
A mod C의 모듈로 역수는 A·B mod C = 1, 즉 A·B ≡ 1 (mod C)를 만족하는 B이다.

오일러 정리
a와 n이 서로소일 때,
a^φ(n) ≡ 1 (mod n) 을 만족한다. 

확장된 유클리드 호제법
두 수 a와 b의 최대공약수를 구하는 것 뿐만 아니라, 그 최대공약수를 a와 b의 선형 조합으로 표현할 수 있는 계수 x와 y, 즉 ax + by = gcd(a, b)를 찾아내는 알고리즘

 

( A + B ) mod C =  ( A mod C + B mod C ) mod C에 대한 증명입니다.   

A = C × Q1 + R1, B = C × Q2 + R2이라고 하면, A mod C = R1, B mod C = R2입니다. 

A + B = C(Q1 + Q2) + R1 + R2이므로, (A + B) mod C = (C(Q1 + Q2) + R1 + R2) mod C입니다. 

그런데 (C(Q1 + Q2) + R1 + R2) mod C 이  형태 어디서 많이 보지 않았나요? 맞습니다.

모듈로 합동 관계 설명에서 보았던 (A + K·C) mod C의 꼴과 같습니다. C의 배수 부분은 삭제 가능하므로 (A + K·C) mod C = A mod C라고 했습니다. 이와 같이 (C(Q1 + Q2) + R1 + R2) mod C = (R1 + R2) mod C 입니다. 

따라서 ( A + B ) mod C =  ( R1 + R2 ) mod C이고, R1 = A mod C, R2 = B mod C이므로

( A + B ) mod C =  ( A mod C + B mod C ) mod C입니다.

 

figure 1-2. 모듈로 연산의 덧셈에 대한 분배법칙 증명

 

 

2. DH(Diffie-Hellman)

DH의 수학적 자물쇠는 '이산 로그' 문제다!

 

DH 등장 배경

 1970년대 초반까지 대칭키 암호화 방식은 치명적인 보안상의 이슈를 가지고 있었습니다. 그 문제는 바로 '키 교환' 과정 중 발생하는 보안 취약점에 있습니다. 대칭키로 데이터를 암호화, 복호화 하기 위해서는 통신의 두 대상자가 동일한 대칭키를 교환해야 하는데, 이 과정에서 제3자가 키를 탈취할 경우 전체 데이터의 보안이 위협받곤 했습니다.

 

 따라서 안전한 대칭키 교환을 위해 키 교환 매체로 정부 기관, 금융 기관 등 신뢰할 수 있는 중개자를 이용하거나 보안 통신 채널을 이용하는 방법을 사용했습니다. 또, 대칭키를 저장한 물리적 매체를 직접 전달하기도 했습니다. 하지만 이런 방식들은 비용이 많이 들고 접근성에 한계가 있다는 단점이 있었습니다. 

 

 이러한 문제를 우아하게 해결하기 위해 1976년 DH(Diffie-Hellman)라는 키 교환 알고리즘이 등장했습니다. DH의 핵심 포인트는 '대칭키의 직접적인 교환 없이도 동일한 대칭키를 나눠 가질 수 있다'는 점인데요, 이게 무슨 말일까요..? DH의 원리를 색상의 조합으로 비유해서 알아봅시다.

 

DH 원리 쉽게 이해하기

 figure 2-1을 보시면 키 파라미터로 회색이 주어지고, A와 B는 각각 분홍색과 하늘색의 개인키를 생성 후 키 파라미터와 혼합하여 공개키를 생성합니다. 그 후 공개키를 맞교환하여 얻은 상대의 공개키와 자신의 개인키를 조합해 서로 같은 색깔의 대칭키를 만들어냅니다. 제3자가 공개키를 탈취한다고 하더라도 개인키의 색깔을 모르면 대칭키의 색깔을 알아맞추는 것은 불가능에 가깝습니다. 또, 클라이언트와 서버가 주고받은 공개키는 대칭키 생성의 재료일 뿐, 대칭키 그 자체는 아닙니다. 대칭키를 교환하지 않고도 서로 같은 대칭키를 공유할 수 있다니 너무 신기하지 않나요?!

 

 

figure 2-1. DH 알고리즘 원리

 

DH가 이산로그를 어떻게 사용하길래?

 DH의 안정성은 '이산 로그' 문제의 난해함을 기반으로 합니다. 이산 로그 문제란, g^x ≡ y (mod p)인 x를 찾는 문제입니다. 위 모듈로 연산에서 학습한 바를 적용해보면 'g를 x제곱한 결과를 p로 나눈 나머지가 y를 p로 나눈 나머지와 같다'라는 조건을 만족하는 x를 찾아내는 것이죠. 지수 계산은 쉽지만 그 역 연산인 이산 로그 계산은 쉽지 않습니다.

 

 예를 들어 g는 3, y는 4, p는 5라고 하겠습니다. x에 1을 대입해보면 3의 1 제곱인 3을 5로 나눈 나머지는 3이므로 4를 5로 나눈 나머지인 4와 다릅니다. 틀렸습니다. 다음으로 x에 2를 대입해보겠습니다. 3의 2제곱인 9를 5로 나눈 나머지는 4이므로 맞았습니다! 운 좋게 2번만에 문제를 풀었네요. 하지만 g와 p가 아주 커진다면 어떨까요? x를 구하는 시간은 기하급수적으로 증가하게 될 것입니다.

 

 478923948를 77232917로 나눈 나머지가 87의 x제곱을 77232917로 나눈 나머지와 동일한 조건을 만족하는 x를 찾는다고 상상해봅시다. 우엑 p가 8자리만 되어도 어지러운데 DH 알고리즘에서는 p를 300자리 이상의 소수로 설정하기를 권고합니다. 소수라는 조건은 또 왜 붙을까요? 만약 p가 소수가 아니라면 p와 g 사이에 공약수가 존재할 수 있고, g^x mod p가 생성할 수 있는 값이 한정되어 반복되는 패턴을 보임으로써 x를 찾기 쉽게 만들 수 있습니다. 

 

 여기서 x는 공개되지 않는 개인키를 가리킵니다. 즉, 개인키가 없다면 방금 한 것 처럼 이산로그 문제를 직접 풀어야 한다는 얘기죠! 조금 전 'DH 쉽게 이해하기'에서 DH의 원리를 색상의 조합으로 설명했던 것 기억나시나요? 그 그림을 바탕으로 아래 figure2-2와 같이 모듈로 연산을 이용한 대칭키 생성 과정을 시뮬레이션 해보겠습니다.

 

 

DH 대칭키 생성 과정

① 키 파라미터 공유

 A와 B는 키 파라미터 p, g를 공유합니다. g는 모듈로 연산에서 사용될 피제수의 밑, p는 제수입니다. g는 1 <= g <= p-1을 만족하는 정수이며, p는 최소 300자리의 소수입니다. 

 

② 개인키 선택

 A와 B가 각각 무작위로 개인키 a와 b를 선택합니다. 개인키는 절대 외부로 노출되어서는 안 됩니다. 

 

③ 공개키를 계산해 맞교환

 g에 자신의 개인키를 제곱한 수를 p로 나눈 나머지를 계산해 공개키를 만들어 서로 교환합니다. A의 공개키는 g^a mod p, B의 공개키는 g^b mod p입니다. 

 

④ 대칭키 계산

 상대로부터 받은 공개키를 피제수의 밑으로, 자신의 개인키를 피제수의 지수로 하는 수를 p로 나눈 나머지를 계산하여 대칭키를 구합니다. A는 (g^b mod p)^a mod p, B는 (g^a mod p)^b mod p를 계산합니다. 모듈로 연산 거듭제곱 법칙에 따라 A의 대칭키는 (g^b)^a mod p = g^ba mod p, B의 대칭키는 (g^a)^b mod p = g^ab mod p이므로 A와 B가 동일한 대칭키를 나눠갖게 되었습니다!

 

figure 2-2. DH 알고리즘 원리 상세

☝🏻 그렇다면 중간자가 공개키를 탈취하면 대칭키를 구할 수 있을까요?

 g^a mod p와 g^b mod p를 알게 되었다고해도 모듈로 연산 분배 법칙에 따라 (g^a + g^b) mod p, (g^a - g^b) mod p, g^(a+b) mod p값만 구할 수 있을 뿐, g^ab mod p값은 구할 수 없습니다. 

 

 

DH 대칭키 생성 예제

그렇다면 실제 값을 대입해 예제를 풀어보겠습니다. 실습을 도와줄 고전적인 인물들을 불러보죠. 클라이언트 Alice, 서버 Bob, Alice와 Bob의 대화를 도청하는 중간자 Eve가 왔습니다. 👏🏻

 

① 키 파라미터 공유

 모듈로 연산에 대한 피제수의 밑 g 값으로 3, 제수 p값으로 17을 공유합니다.

 

② 각각 개인키 a, b 선택

 Alice는 개인키를 15, Bob은 개인키를 13으로 선택했습니다.

 

③ 공개키를 계산해 맞교환

 Alice는 공개키로 3의 15제곱을 17로 나눈 나머지를 Bob에게 보냅니다. Bob은 3의 13 제곱을 17로 나눈 나머지를 Alice에게 보냅니다.

 

④ 대칭키 계산

 Alice는 Bob에게 받은 공개키(3^13 mod 17)의 15제곱을 17로 나눈 나머지를 계산해 (3^13)^15 mod 17, 즉 3^195 mod 17을 대칭키로 얻고, Bob은 (3^15 mod 17)^13 mod 17를 계산해 (3^15)^13 mod 17, 동일하게 3^195 mod 17를 얻습니다. Alice의 경우 3^13 mod 17을 먼저 계산해서 12를 얻은 후 12^15 mod 17을 계산하고, Bob의 경우 3^15 mod 17를 계산 후 6을 얻은 후 6^13 mod 17 계산해봐도 대칭키 값은 모두 10으로 동일합니다. 이제 Alice와 Bob은 동일한 대칭키로 데이터를 암호화해서 통신할 수 있게 되었습니다.

 

 Eve는 열심히 도청해서 키 파라미터 3, 17, 공개키 6, 12를 알아내었지만 Alice와 Bob이 꽁꽁 숨긴 개인키는 알아낼 수 없었기에 브루트 포스 어택으로 대칭키를 추적 계산하다가 배가 고파서 그만 두었습니다.

 

figure 2-3. DH 알고리즘 대칭키 생성 과정 예제

https://ko.symbolab.com/solver/modulo-calculator에서 모듈로 연산을 직접 해볼 수 있어요!

 

 

3. RSA(Rivest-Shamir-Adelman)

RSA의 수학적 자물쇠는 '소인수 분해' 문제다!

 

RSA 등장 배경과 사용 범위

 1978년에는 RSA(Riveset-Shamir-Adelman)가 등장하며 비대칭키 암호화 방식이 본격적으로 사용되기 시작했습니다. RSA는 '디지털 서명'이 가능한 최초의 알고리즘으로, 키 교환 알고리즘으로만 쓰이는 DH와 달리 전자 상거래, 데이터 암호화, 키 교환 등에도 광범위하게 사용됩니다. 주고받을 메세지를 암호화할 수도 있고, 인증기관이 자신의 개인키로 서버의 정보와 서버의 공개키를 암호화함으로써 디지털 서명을 할 수도 있고, 브라우저가 서버의 공개키로 대칭키를 암호화해서 서버와 키 교환을 할 수도 있습니다.

 

 하지만 RSA는 키 교환 및 메세지 암호화 알고리즘으로는 부적합한데요, 복잡한 연산으로 인해 속도가 느리기 때문입니다. 완벽한 암호화 알고리즘은 없기 때문에 제 아무리 RSA로 암호화된 데이터라고 하더라도 제3자(중간자)에 의해 복호화될 위험성이 있고, 키의 크기를 증폭시키는 방법으로 보안성을 향상시키면 연산의 복잡성이 더욱 커져서 네트워크 지연을 발생시킵니다. 따라서 재빠른 네트워킹을 요하는 메세지 송수신 및 키 교환 시에는 RSA 대신 주로 AES 블록 암호화 알고리즘과 DH 키 교환 알고리즘을 사용합니다.

 

RSA 원리 쉽게 이해하기

 RSA가 어떻게 비대칭키로 데이터를 암호화하고 복호화하는지는 아래 그림 figure 3-1을 참고해주세요. 암호화는 디지털 서명, 복호화는 서명 검증 과정과 같습니다.

 

 B는 공개키-개인키로 구성된 '비대칭키' 한 쌍을 생성합니다. A가 B에게 데이터를 보낼 때 A는 B의 열린 자물쇠(B의 공개키)를 받아 데이터를 암호화합니다. 그 자물쇠를 열 열쇠는 오직 B만이 가지고 있는 B의 개인키입니다. 이제 A가 자물쇠를 닫아 데이터를 암호화해서 B에게 보내면 B는 잠겨있는 자신의 자물쇠를 자신의 개인키로 열어 데이터를 복호화할 수 있는 구조입니다. 엄밀히 말하면 그 자물쇠가 공개'키'이긴 하지만, 공개키로 암호화한 데이터는 트랩도어인 개인키를 사용하거나 일방향 함수를 역산해야 열리는 '자물쇠'처럼 작동합니다.

 

 트랩도어는 안에서는 열기 쉽지만 밖에서는 발견하기도, 열기도 어렵습니다. RSA는 일방향 함수의 일종인 트랩도어 함수이며, 트랩도어 함수는 일방향 함수와 마찬가지로 역 연산이 어렵지만 트랩도어가 있으면 역 연산을 쉽게 수행할 수 있습니다. 그러니 통신의 두 참여자 A와 B를 제외한 제3자로부터 데이터를 안전하게 보호하기 위해서는 트랩도어, 즉 개인키를 절대 사수해야겠쥬?

 

figure 3-1. RSA 알고리즘 원리(왼쪽 이미지 출처: 저요, 오른쪽 트랩도어 이미지 출처: https://build.com.au/trapdoors)

RSA의 소인수분해 사용법

 DH가 '이산 로그' 문제의 난해함에 기인해 만들어진 알고리즘이라면, RSA는 '소인수 분해'를 사용합니다. 소인수 분해 역시 일방향 함수의 특성을 활용합니다. 소인수 분해는 그리 어려운 개념이 아니니 자세히 언급하지는 않겠습니다. figure3-2의 N이 서로소인 비밀값 p와 q의 곱으로 이루어진 합성수이며, N으로부터 p와 q를 알아내려고 할 때 소인수 분해를 해야 합니다. p와 q의 값을 비밀에 부치는 것이 RSA 보안의 핵심이며, p와 q의 곱인 N의 크기에 따라 RSA의 보안성이 결정됩니다.

 

 RSA를 통해 통신의 당사자가 암호화된 데이터를 주고받는 세부 과정은 다음과 같습니다. 먼저 B가 공개키 <N, e>와 개인키 <N, d>로 이루어진 비대칭키 쌍을 생성합니다. 개인키는 잘 숨겨둡니다. 그 후 B의 공개키를 A에게 전달합니다. A는 암호화할 메세지를 m으로 변환한 후 m을 B의 공개키<N, e>로 암호화해서 암호문 C를 만듭니다. C=m^e mod N입니다. 암호문 C를 받은 B는 자신의 개인키 <N, d>로 m을 복호화합니다. C^d mod N를 계산하면 다시 평문 m을 구할 수 있게 됩니다. p, q를 모른다면 e를 알아도 d는 특정할 수 없습니다.

 

figure 3-2. RSA 알고리즘 원리 상세

 지금부터 C^d mod N을 계산하면 진짜루 m이 나오는지 증명해볼까요?! 호호

 

RSA 비대칭키 암호화-복호화 증명

① 비대칭키 쌍 생성

 공개키 <N, e>, 개인키 <N, d>로 구성된 비대칭 키를 생성합니다.

 

 [N 생성]

  B는 서로소이면서 최소 1024 bit인 p와 q를 곱해 합성수 N을 만듭니다. N은 암호화, 복호화 시 수행하는 모듈로 연산의 제수이며, 공개되는 값이지만 이 수의 서로소인 p와 q는 절대 알려져서는 안 됩니다. 비밀값 d를 계산해낼 수 있기 때문입니다.

 

 [e 선택]

  다음으로 1 < e < φ(N)을 만족하며, φ(N)과 서로소인 정수 e를 선택합니다. e값으로는 보통 3, 17, 65537 중 하나를 사용한다고 합니다. φ(N)는 '오일러 파이 함수'이며, 1부터 N까지의 정수 중에서 N과 서로소인 정수의 개수를 반환합니다. p와 q가 서로소일 때 φ(N)=(p-1)(q-1)입니다.

 

 [d 선택]

  마지막으로 e mod φ(N)의 모듈로 역수 d를 선택합니다. ed mod φ(N) = 1을 만족하는 d를 고르면 됩니다. d는 '확장된 유클리드 호제법'을 통해 빠르게 구할 수 있습니다. 확장된 유클리드 호제법을 사용하지 않는다면 0부터 mod φ(N) - 1까지의 값들을 하나씩 대입해 d를 찾아내야 합니다. 

 

② 키 분배

  안전하지 않아도 되는 통신 채널로 B가 A에게 자신의 공개키 <N, e> 를 전달합니다.

 

③ 암호화 m^e mod N = C

  A는 padding scheme 변환법을 통해 메세지를 N보다 작고 N과 서로소인 정수 m으로 만듭니다. 그 후 B의 공개키의 e, N값을 가져와 암호문 C를 만들어 B에게 보냅니다. C는 m^e mod N 입니다. padding scheme 변환법에 대해서는 설명하지 않겠습니다.

 

④ 복호화 m = C^d mod N

 B는 자신의 개인키 <N, d>를 가져와 암호문 C를 복호화합니다. 앞서 암호문 C를 평문 m으로 복호화하기 위해서는 C^d mod N값을 구한다고 했습니다. 그럼 C^d mod N의 연산의 결과는 무엇인지, 최종적으로 m은 어떻게 도출되는지 알아보겠습니다.  

 

C^d mod N = (m^e mod N)^d mod N = (m^e)^d mod N = m^ed mod N

먼저 C^d mod N = (m^e mod N)^d mod N입니다. 여기서 (m^e mod N)^d mod N은 모듈로 연산 거듭제곱 법칙에 따라 (m^e)^d mod N과 같습니다. C^d mod N가 m^ed mod N으로 정리되었군요!

 

 m^ed mod N = m^(k·φ(N) + 1) mod N = (m^(k·φ(N))×m) mod N = ((m^φ(N))^k) mod N × m mod N) mod N

 ed값은 어떻게 구해야할까요? 이전에 비대칭키 쌍을 생성하면서 d를 e mod φ(N)의 모듈로 역수로 선정한 바 있습니다. 따라서 ed mod φ(N) = 1이며, 임의의 값 k에 대해서 ed = k·φ(N) + 1라고 할 수 있습니다. 그렇다면 m^ed mod N = m^(k·φ(N) + 1) mod N입니다. m^(k·φ(N) + 1) mod N는 다시 말해 (m^(k·φ(N))×m) mod N이고, (m^(k·φ(N))×m) mod N은 모듈로 연산 분배법칙에 따라서 ((m^(k·φ(N)) mod N × m mod N) mod N입니다.

 

((m^φ(N))^k) mod N × m mod N) mod N =  (1^k) mod N × m mod N = m mod N

 ((m^(k·φ(N)) mod N × m mod N) mod N에서 m^(k·φ(N)) mod N은 ((m^φ(N))^k) mod N과 같습니다. ((m^φ(N))^k) mod N은 모듈로 연산 거듭제곱 법칙에 따라 (m^φ(N) mod N)^k mod N이며, 평문 m 암호화 시 m을 N과 서로소인 수로 골랐으므로 m^φ(N) mod N은 오일러 정리에 따라서 1입니다. ((1^k) mod N × m mod N) mod N = (1 × m mod N) mod N이고, 모듈러 연산 결합법칙에 따라 (m mod N) mod N = m mod N입니다.

 

 결과적으로 C^d mod N = m^ed mod N = m mod N이 도출되었습니다. 그리고 m은 N과 서로소이면서 N보다 작은 정수이므로 m을 N으로 나눈 나머지는 m과 같습니다. 즉, m mod N = m입니다. 드디어 암호문 C를 평문 m으로 복호화했습니다!! 🥳

 

figure 3-3. RSA 비대칭키 암호화 알고리즘 증명

 마지막으로 실제 숫자를 대입해서 C^d mod N = m이 정말 맞는지 확인해보겠습니다. 

 

RSA 비대칭키 암호화-복호화 예제

① 비대칭키 쌍 생성

  [N 생성]

   p = 11, q = 3    # 예제이므로 계산하기 쉬운 작은 값을 선택하겠습니다.

   N = 33   # p x q

 

 [e 선택] 

   φ(N) = 20   # (p-1)(q-1)

   e = 7   # 1보다 크고 φ(N)보다 작은  수 중 φ(N)와 서로소인 정수

 

 [d 선택]

   d = 3   # ed mod φ(N) = 1을 만족하는 정수

 

 공개키 <33, 7>, 개인키 <33, 3>

 

② 키 분배

   통신 채널로 B가 A에게 자신의 공개키 <33, 7> 전달

 

③ 암호화 m^e mod N = C

   m = 5   # N보다 작고 N과 서로소인 자연수

   C = 5^7 mod 33 = 14

 

④ 복호화 m' = C^d mod N

   m' = 14^3 mod 33 = 5

 

👉🏻 C^d mod N = 5로 m과 동일합니다. 

 

 

 

 

4. 자물쇠를 새로 만들어버린다면 어쩔건데?

 예..? 자물쇠를 풀기는 어려우니 그냥 새로 만들어버리겠다구요? 새로 만들어서 Alice와 Bob의 중간에서 Alice에게는 Bob인 척, Bob에게는 Alice인 척 하겠다구요??!😱 그런 방법이 있었군요.... 중간자 Eve가 자신의 공개키를 만들어 Alice와 Bob이 자신의 공개키를 사용하게 만든다면 자신의 개인키로 손쉽게 데이터를 복호화할 수 있고, 변조한 데이터를 보낼 수도 있다는 점이 DH와 RSA의 취약점입니다.

 

 이렇게 Eve가 각성한 상황은 어떻게 대비해야 할까요. Alice와 Bob이 서로의 신원을 확인해야 합니다. 서명과 그에 대한 검증을 하는 것이죠. 또 키를 빠르게 갱신하면 아무리 Eve가 작정했더라도 매번 키 갱신 시점마다 새로운 자물쇠를 생성해 Alice와 Bob을 속일 수는 없을 것입니다. 또, 중요한 데이터를 난독화하는 방법을 생각해볼 수 있겠네요.

 

 

DH & RSA 공통 보완점

PKI를 통해 인증된 공개키 사용

 공개키는 비대칭키 알고리즘의 핵심 개념이며, 상대의 공개키를 사용해 비밀값을 생성합니다. 그리고 그 비밀값은 상대와 공유하게 됩니다. 참고로 DH에서의 비밀값은 각자 생성한 대칭키이며, RSA에서의 비밀값은 암호화한 데이터를 의미합니다. 만약 그 공개키가 중간자의 것이라면 공개키로 만든 비밀값은 중간자만이 복호화할 수 있는 데이터가 됩니다.

 

 이미 통신 채널로 교환되고 있는 비밀값을 해독하기는 어렵지만, 중간자가 통신의 당사자로 참여해 도청 대상이 자신의 공개키를 사용하도록 만들어버리면 비밀값을 해독할 필요도 없이 자신의 개인키로 비밀값을 얻을 수 있습니다. 따라서 공개키로 데이터를 암호화해서 주요 정보를 주고받을 때는 출처가 명확한 공개키를 사용하는 것이 중요합니다.

 

 그리고 그 출처를 인증하는 시스템은 PKI가 제공합니다. PKI는 Public Key Infrastructure의 약자로, 디지털 상에서 관리되는 공개키와 개인키 쌍들을 안전하게 생성, 배포, 관리, 폐기하는 시스템입니다. PKI를 통해 공개키가 인증되면 해당 공개키를 신뢰할 수 있고, 안심하고 해당 공개키로 비밀값을 만들어 송신할 수 있게 됩니다.

 

 

DH 보완점

일회용 키 사용 - Perfect Forward Secrecy

 세션마다 개인키를 새로 선택해서 그에 대한 공개키와 대칭키를 일회용으로 만들면 어떨까요? 중간자가 특정 시점의 키를 탈취하더도 해당 시점 이전이나 이후의 통신 내용은 복호화할 수 없을 것입니다. 이렇게 일회용 키를 사용하는 보안 메커니즘을 Perfect Forward Secrecy, 줄여서 PFS, 또는 Perfect를 빼고 FS라고도 합니다.

 

RFC 8446(TLS 1.3)에 따르면 TLS 1.3부터는 figure 4-1과 같이 키 교환 방식에서 RSA와 DH가 사라지고 Forward Secrecy를 지원하는 DHE(Diffie-Hellman Ephemeral)와 ECDHE(Elliptic Curve Diffie-Hellman Ephemeral)가 사용됩니다. 공통적으로 사용되는 단어인 'Ephemeral'은 '일시적인' 이라는 의미로, Forward Secrecy가 지향하는 바와 일맥상통합니다.

 

figure 4-1. TLS 1.3부터 키 교환 방식에서 RSA와 DH가 삭제됨(RFC 8446)

 

 

RSA 보완점

이중 암호화

 데이터 송신자의 신원과 데이터의 무결성을 보증받을 수 있는 방법도 있습니다. 바로 이중 암호화를 하는건데요, 이중 암호화는 기존 암호화 방식대로 상대의 공개키로 원본 데이터를 암호화한 후 한번 더 자신의 개인키로 데이터 해시값을 암호화하는 작업입니다. 데이터의 해시값을 개인키로 암호화하는 과정을 '디지털 서명'이라고 하며, 수신자는 디지털 서명을 '검증(Verification)'함으로써 데이터가 믿을 수 있는 대상으로부터 왔고, 데이터가 무결하다는 것을 확인할 수 있습니다. 

 

 이중 암호화와 복호화의 과정은 figure 4-2와 같습니다. A와 B는 공개키를 주고받습니다. 송신자 A는 데이터 원본을 B의 공개키로 암호화하고, 데이터의 해시값을 계산해서 해당 해시값을 자신의 개인키로 암호화하여 디지털 서명을 생성합니다. 이렇게 이중 암호화된 데이터를 받은 B는 A의 공개키로 A의 디지털 서명을 검증하고, 자신의 개인키로 데이터를 복호화하게 됩니다. 만약 A가 보낸 데이터가 아니라면 A의  공개키로 서명을 검증할 수 없을 것입니다.

 

figure 4-2. 디지털 서명-검증 과정이 포함된 RSA 이중 암호화

 

데이터 난독화

 키를 탈취해서 데이터를 한 번 복호화하더라도 그 복호화된 데이터가 난독화되어있다면 원본 데이터는 얻기 힘들어집니다. 데이터를 난독화하는 알고리즘에는 해시, 솔트, 페퍼가 있습니다. 해시가 일반적으로 사용되며, 여기에 솔트와 페퍼까지 추가하면 복호화의 난이도가 더 올라가겠죠?

 

 해시는 데이터를 고정된 크기의 유일한 값으로 요약하는 암호화 처리 과정입니다. 해시 함수는 하나의 입력값에 대해서 항상 동일한 출력값을 가지기 때문에 해커들은 자주 사용되는 입력값과 그에 대한 해시값을 리스트업 해놓은 레인보우 테이블을 만들어 놓습니다. 만약 레인보우 테이블에 원본 데이터와 일치하는 입력값이 존재한다면, 손쉽게 해시 결과값을 유추할 수 있게 됩니다. 따라서 이러한 취약점을 보완하기 위해 해시를 한 번 더 난독화할 필요가 있습니다. 

 

 솔트는 각 데이터에 고유하게 추가되는 무작위 문자열로, 동일한 해시값을 갖는 하나의 입력값에 사용자별로 서로 다른 무작위 문자열을 추가함으로써 레인보우 테이블 공격을 예방하는 데에 도움이 됩니다. 이와 비슷한 개념의 페퍼도 있으며, 페퍼는 하나의 시스템 전체에 걸쳐 동일하게 사용되는 무작위 문자열입니다. 페퍼는 선택적인 보안 강화 수단으로, 솔트와 함께 사용함으로써 데이터의 보안성을 더욱 향상시킬 수 있습니다.

 

 

 

5. 마무리

 비대칭키 알고리즘에 대해서 공부하면서 수학적인 원리로 이렇게나 견고한 암호화 체계를 만들 수 있다는 게 정말 신기했습니다. 사실 이 포스팅을 하게 된 계기는 대표적인 비대칭키 알고리즘인 DH와 RSA가 서로 다른 사용 목적을 가진 이유가 궁금해서였습니다. 각 알고리즘을 이해하려고 하다보니 흘러흘러 그 수학적 원리까지 다루게 되었는데, 핵심은 각각의 장단점이 있어 사용하기 적합한 범위가 다르고, 둘 다 일방향 함수의 특성을 사용한 비대칭키 방식이기 때문에 복호화하기 어렵지만, 중간자 공격에는 취약하기 때문에 서로의 신원을 확인하거나 데이터 이중 암호화 + 난독화 등의 보완이 필요하다는 것이었습니다. 아래 표로 DH와 RSA를 비교하며 마무리해보도록 하겠습니다.

 

		DH(Diffie-Hellman)	RSA(Riveset-Shamir-Adelman)
공통점		- 비대칭키 방식으로 동작 - 일방향 함수의 특성 사용
차이점	사용 목적	- 대칭키 생성	- 디지털서명과 검증 - 암호화와 복호화
	사용 범위	- 키 교환	- 디지털 서명 - 데이터 암호화 - 키 교환 ...
	장점	- 직접적인 키 교환 없이 안전하게 대칭키 생성 - RSA 키 교환 알고리즘에 비해 빠른 속도	- HTTPS 뿐만 아니라 이메일, VPN 등 다양한 보안 통신 프로토콜에 광범위하게 적용 가능
	단점	- 디지털 서명과 검증 기능 부재	- 키 길이에 의존하는 보안성 - 복잡한 연산으로 인한 느린 계산 속도 및 막대한 컴퓨팅 리소스 소모
중간자 공격 대비 방법		- PKI(Public Key Infrastructure)를 통해 인증된 공개키 사용
		- 일회용 키 사용  (forward secrecy를 지원하는 DHE, ECDHE   알고리즘 사용)	- 데이터 이중 암호화   (상대 공개키로 암호화 + 자신의 개인키로 암호화(서명)) - 데이터 난독화(해시, 솔트, 페퍼)

 

 

 추가로 본문에서 다음과 같은 의문점이 남으신 분들은 링크를 참고해주세요!

🙋🏻‍♀️ '디지털 서명'.. 뭔데? 
      → [HTTPS] SSL/TLS Handshake란? - '서버 인증서 발급(feat. PKI)',  '브라우저의 인증서 검증' 
 🙋🏻‍♀️ HTTPS에서 사용되는 '암호화 기술들을 카테고리화' 하고 싶어! 
      → [Cipher Suite] 안전한 데이터 전송을 위한 SSL/TLS 기술 집약체

 

 

 

6. Reference

• 모듈로 연산
  
  • https://ko.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/what-is-modular-arithmetic
  • https://ko.wikipedia.org/wiki/%EB%AA%A8%EB%93%88%EB%9F%AC_%EC%82%B0%EC%88%A0
  • https://deepdata.tistory.com/577

 

•  DH
  • https://ko.khanacademy.org/computing/computer-science/cryptography/modern-crypt/v/diffie-hellman-key-exchange-part-2
  • https://tramamte.github.io/2018/07/20/diffie-hellman/
  • https://ko.wikipedia.org/wiki/%EB%94%94%ED%94%BC-%ED%97%AC%EB%A8%BC_%ED%82%A4_%EA%B5%90%ED%99%98#:~:text=%EB%94%94%ED%94%BC%2D%ED%97%AC%EB%A8%BC%20%ED%82%A4%20%EA%B5%90%ED%99%98(Diffie,1976%EB%85%84%EC%97%90%20%EB%B0%9C%ED%91%9C%ED%95%98%EC%98%80%EB%8B%A4.

 

•  RSA
  
  • https://tramamte.github.io/2018/07/25/rsa/
  • https://m.blog.naver.com/at3650/220098716837
  • https://gngsn.tistory.com/96
  • https://ko.wikipedia.org/wiki/RSA_%EC%95%94%ED%98%B8