[정글 WEEK06_RB-Tree] 기본 개념 - 특성

 

자가 균형 이진 탐색 트리(Self-Balancing Binary Search Tree)의 일종인 RB Tree(Red-Black Tree)를 알아보자.

---

특성

레드블랙 트리는 노드 삽입, 삭제 시 색깔 규칙과 회전 연산을 통해

루트 노드에서 NIL 노드까지의 경로에 있는 블랙 노드의 개수를 제한함으로써 균형을 유지한다.

어떤 경로도 다른 경로보다 두배 이상 길지 않음을 보장하며, 모든 동적 집합 연산을 트리의 높이에 비례해서 O(log n) 시간에 수행한다.

 

"어떤 트리에서 루트 노드부터 NIL 노드까지 가는 경로 중 가장 짧은 경로는 블랙 노드로만 N개(bh(x))로 구성된 경로이며,
 가장 긴 경로는 N개의 블랙 노드와 N개의 레드 노드가 번갈아 나오는 경로로 2N(2*bh(x))개의 노드로 구성된다.
 따라서 가장 긴 경로가 가장 짧은 경로의 2배를 넘지 않는다."

 

 

🧮 대표적인 동적 집합 연산 6가지

• Search(S, k): 집합 S에서 키 k를 가진 원소 찾기

• Insert(S, x): 원소 x를 집합 S에 추가하기

• Delete(S, x): 원소 x를 집합 S에서 삭제하기

• Minimum(S): 집합 S에서 가장 작은 키를 가진 원소 찾기

• Maximum(S): 집합 S에서 가장 큰 키를 가진 원소 찾기

• Successor(S, x): x보다 조금 더 큰 값 찾기

• Predecessor(S, x): x보다 조금 더 작은 값 찾기

 

 

🛡️ 레드블랙 트리 성립 조건

❗️아래 조건을 모두 만족해야 한다.

1️⃣ 모든 노드는 적색 또는 흑색이다.

2️⃣ 루트는 흑색이다.

3️⃣ 모든 리프(NIL) 노드들은 흑색이다.

4️⃣ 부모 노드가 적색이면 그 노드의 자식들은 모두 흑색이다. 부모 자식이 동시에 적색 노드일 수 없다. (red-red violation)

     → 부모가 흑색이라면 자식 모두 적색이어도 괜찮다. 적색 노드는 반드시 검정 부모를 가짐

5️⃣ 특정 노드로부터 해당 노드의 리프들로 가는 모든 경로들은 모두 같은 수의 흑색 노드를 포함한다. (흑색 높이 균일)

     → 루트 노드에서 NIL 노드까지의 모든 경로의 수는 블랙 노드의 수와 같다.

 

 

🆚  레드블랙 트리 vs AVL 트리

레드블랙 트리를 또다른 자가 균형 이진 탐색 트리인 AVL 트리와 비교하면 다음과 같다.

항목	레드블랙 트리	AVL 트리
균형 정도	비교적 느슨함	매우 엄격함(항상 거의 완벽한 균형)
삽입/삭제 비용	회전이 적어 상대적으로 효율적	회전과 높이 갱신이 많아 상대적으로 비용이 큼
회전 수	최대 2회(삽입/삭제 시)	최대 4회(삭제 시)
활용 방안	안정적인 성능을 원할 때 → Java의 TreeMap, TreeSet, C++의 set, map 등 라이브러리에서 사용	탐색이 자주 발생하거나 빠른 검색이 중요할 때 → 일부 데이터베이스 인덱스, 검색 최적화 등에서 사용
노드당 메모리 사용량	색 정보(1bit)	서브트리의 높이(5~6 bits) 또는 균형 인수(최소 2bits)
성능	모든 동적 집합 연산에 대해서 항상 O(log n) 보장

 

📁 레드블랙 트리 용어 정리

[기본]

Node(노드): 트리 안에 들어 있는 하나의 데이터 단위. 값, 자식 포인터, 부모 포인터, 색 정보 등을 가짐

Black Node(검정 노드): 색이 검정인 노드. 레드블랙 트리의 균형을 위한 기준

Red Node(빨강 노드): 색이 빨강인 노드. 연속해서 등장할 수 없음(Red-Red violoation)

Root(루트 노드): 트리의 가장 위에 있는 노드. 항상 검정이어야 함

Leaf(리프 노드) = NIL 노드: 리프를 표현하는 특수한 빈 노드. 항상 검정색이어야 함

Sentinel(경계 노드): 다수의 NIL 노드 대신에 하나의 Sentinel만 만들어줌

Parent(부모): 특정 노드의 바로 위 노드

GrandParent(조부모): 부모의 부모. 삽입/삭제 시 구조 수정할 때 자주 등장함

Uncle(삼촌): 부모의 형제 노드. 즉, 부모의 부모의 다른 자식

Sibling(형제): 같은 부모를 가지는 다른 노드. 삭제 후 균형 복구 시 등장함

 

[균형 관련 용어]

Black height(검정 높이): 특정 노드에서 NIL까지 가는 경로에서 만나는 검정 노드의 수(자기 자신 제외). 같은 노드에서 시작하는 모든 경로의 검정 높이는 동일해야 함. bh(x)로 표현

Red-red violoation(빨강-빨강 위반): 특정 노드와 그 부모가 모두 빨강일 경우 발생. 반드시 회전이나 색 변경으로 해결해야 함

Balancing(균형): 삽입/삭제 등으로 인해 트리 구조가 깨졌을 때, 회전/색 변경을 통해 규칙을 복구하는 과정

 

[회전 관련 용어]

Rotation(회전): 트리의 모양을 변경하는 연산. 구조는 유지하면서 균형을 맞춤

Left rotation(좌회전): 특정 노드 기준으로 오른쪽 자식을 위로 올리고, 해당 노드를 왼쪽으로 내림

Right rotation(우회전): 특정 노드 기준으로 왼쪽 자식을 위로 올리고, 해당 노드를 오른쪽으로 내림

Double rotation(이중 회전): 좌우/우좌 순서로 두번 회전. 색 변경과 함께 진행함

 

[연산 관련 용어]

Insert(삽입): 새로운 값을 트리에 추가하는 연산. 이 때 빨강으로 삽입하고 규칙을 어기면 색 변경/회전으로 복구함

Delete(삭제): 값을 제거하는 연산. 삭제 후 black height가 변할 수 있어서 복잡한 색/회전 복구가 필요함

Insert fix-up(삽입 균형 복구): 삽입 후 균형이 깨진 경우 red-red violoation 등을 해결하는 과정

Delete fix-up(삭제 균형 복구): 삭제 후 검정 노드 수가 달라졌을 때 이를 해결하는 복잡한 절차

Double black(이중 블랙): 삭제 후 검정 노드가 부족하게 된 상황. 이를 해결하기 위해 추가적인 회전이나 색 이동이 필요함 

Transplant(이식): 삭제 시 노드를 다른 노드로 교체하는 과정

 

 

🌲 트리 구조체

트리의 각 노드는 color, key, left, right, parent 등의 필드를 가지며, 아래와 같은 구조체로 정의할 수 있다.

typedef enum { RED, BLACK } Color;

typedef struct _rbnode{
    Color color;            // RED or BLACK
    int key;                // 노드 키 값
    struct _rbnode *left;   // 왼쪽 자식 노드
    struct _rbnode *right;  // 오른쪽 자식 노드
    struct _rbnode *parent; // 부모 노드
} RBNode;

 

 

📌 n개의 노드를 가지는 레드블랙 트리에 대한 수치 정리

항목	수치/범위	설명
트리 높이	<= 2 * log(n + 1)	레드 노드 블랙 노드가 번갈아 나오는 경우
검정 높이	<= log(n + 1)	루트 기준 최대 검정 노드 수
회전 수	삽입 <= 2, 삭제 <= 3	-
적색 노드 비율	<= 최대 50%	Red-Red violoation 규칙으로 인한 제한
NIL 수	= n + 1	NIL 노드는 항상 검정, 고정 개수
메모리	≈ 32bytes / n	포인터 + 색 정보 포함

 

 

✏️ 개념 이해를 위한 연습 문제(Introduction To Algorithms)

1. 키 {1,  2, ..., 15}로 구성된 높이 3의 완전 이진 탐색 트리를 그려라. NIL 노드를 추가하고, 트리에 세 가지 다른 방법으로 색칠해서 흑색 높이가 각각 2, 3, 4인 레드블랙 트리를 만들어라.

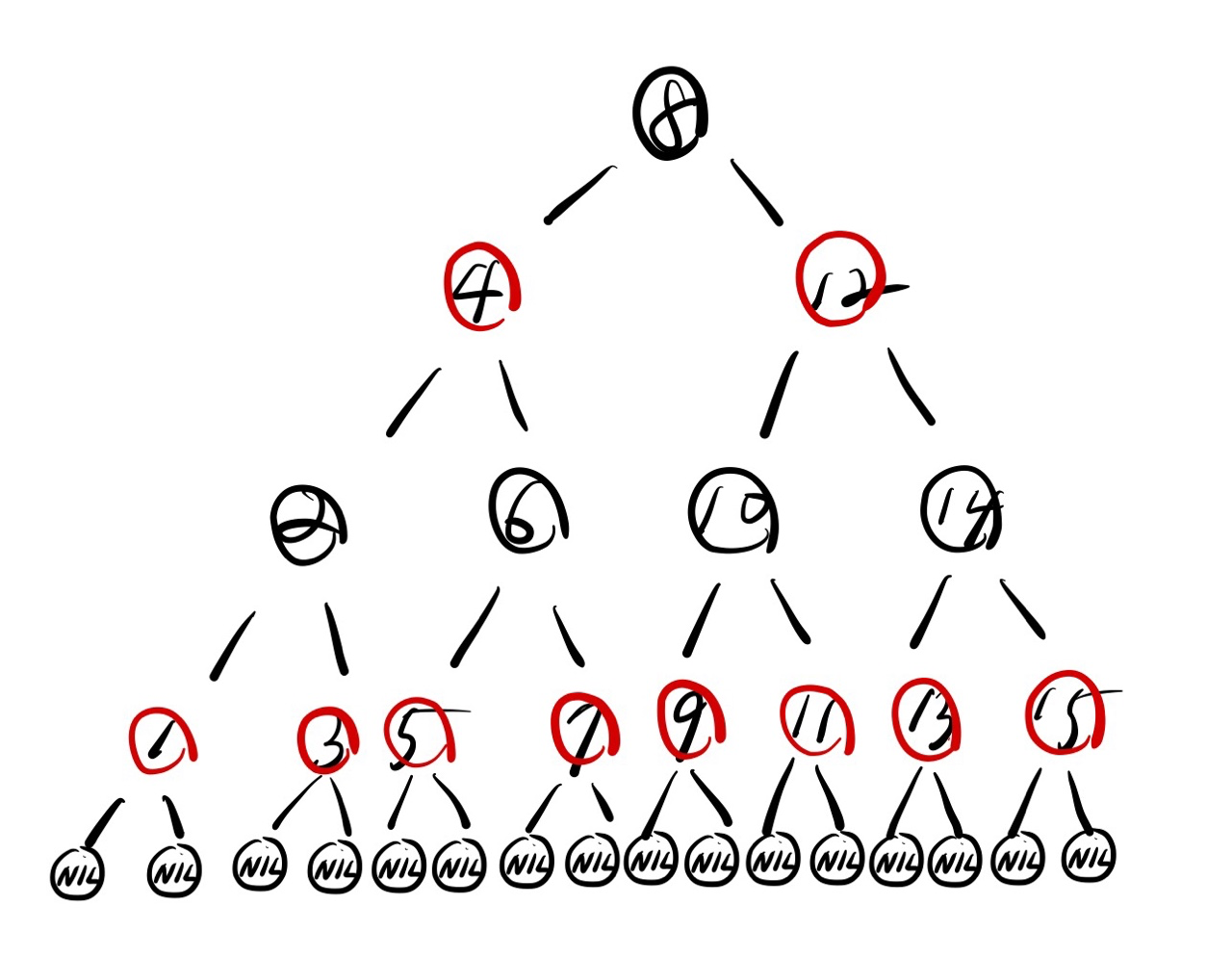
bh(x) = 2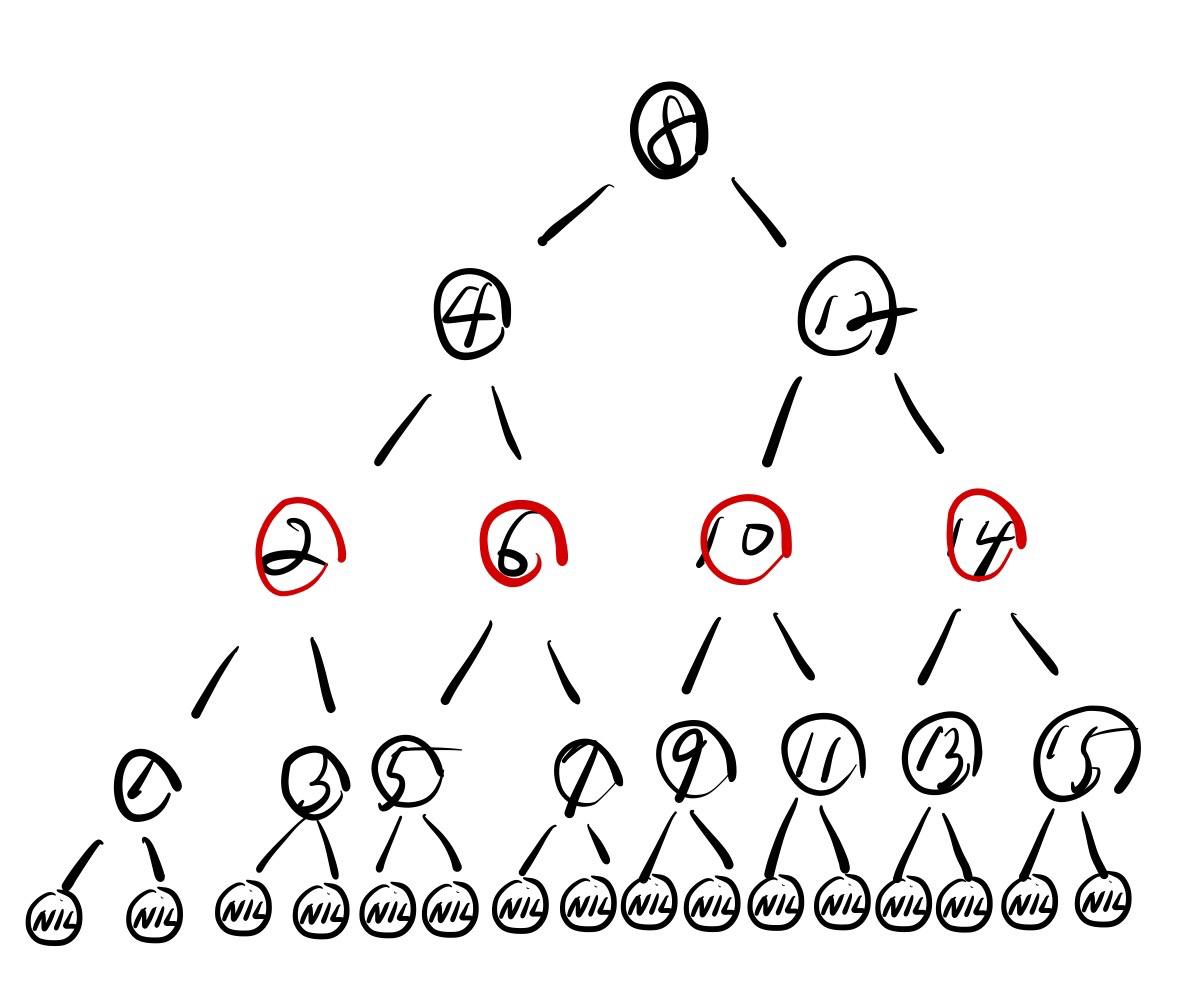

bh(x) = 3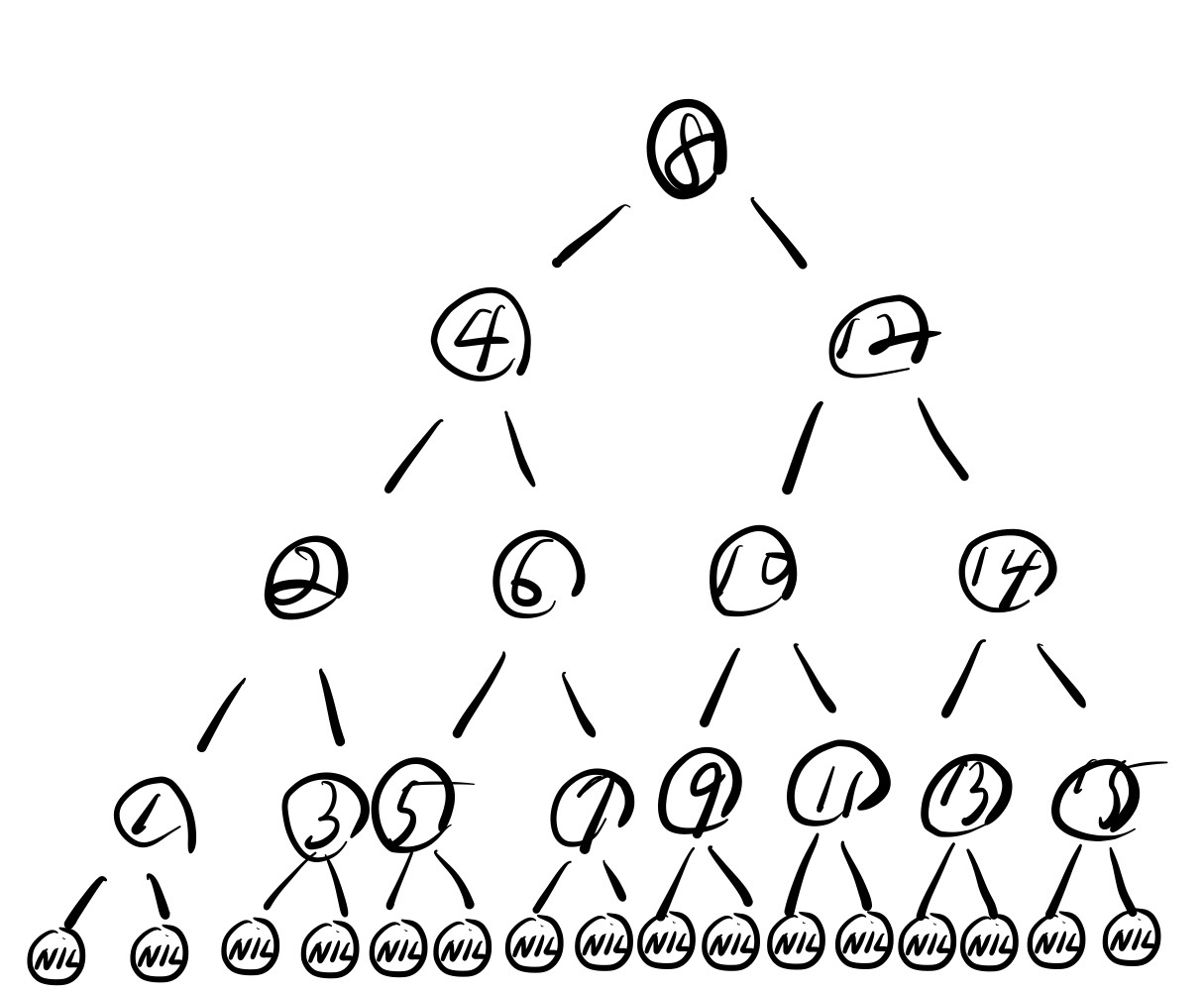

bh(x) = 4

 

2. 레드블랙 트리의 모든 적색 노드를 흑색 부모로 병합해서 적색 노드의 자식이 흑색 부모의 자식이 되는 경우를 생각해보자. 모든 적색 자식이 병합된 후의 흑색 노드의 가능한 차수는 얼마인가? 결과로 만들어지는 트리의 리프들의 깊이에 대해 어떤 판단을 내릴 수 있는가?

 적색 노드를 부모(무조건 블랙 노드)에 병합하면 적색 노드는 반드시 블랙 노드를 자식으로 가지므로, 검정 부모가 4개의 자식을 가지게 된다. 병합 후 한 노드가 최대 4개의 자식을 가지게 되어 2-3-4 트리의 형태를 가진다. 따라서 병합 후의 흑색 노드의 가능한 최대 차수는 4이고, 결과 트리는 2-3-4 트리와 동형이다. 또한, 병합 후 리프 길이는 균등하게 유지된다. 

* 2-3-4 트리: 하나의 노드에 최대의 3개의 값(키), 최대 4개의 자식을 가질 수 있는 균형 다진 트리(M-ary Tree)

 

3. 레드블랙 트리에서 노드 x로부터 자손인 리프에 이르는 최장 단순 경로의 길이가 노드 x로부터 자손인 리프에 이르는 최단 단순 경로의 길이에 비해 항상 두 배 이하임을 보여라.

 특정 노드 x에서 리프까지 가는 경로는 여러 개가 있을 수 있지만 레드 노드는 반드시 블랙 부모를 가진다. 즉, 경로 상에 빨강 노드가 있다면 반드시 검정 노드와 번갈아서 등장한다. 따라서, 최단 경로(Shortest)는 검정 노드만 있을 때이며, 길이는 bh(x)이다. 최장 경로(Longest)는 빨강노드-검정노드가 번갈아 나오는 경우이며, 길이는 최대 2 * bh(x)이다. 따라서 항상 Longest <= 2 * Shortest이다.

 

4. 흑색 높이가 k인 레드블랙 트리의 내부 노드의 가능한 최대 개수는 몇 개인가. 또, 가능한 최소 개수는 몇 개인가?

흑색 높이가 k라면 트리 높이의 최단 길이는 k이고, 최장 길이는 2k이다. 따라서, 트리 노드 최소 개수는 2^k - 1, 최대 개수는 2^(2*k) - 1개 이다.  

 

5. 흑색 내부 노드에 대한 적색 내부 노드의 비율을 최대로 하는 n개의 노드로 이루어진 레드블랙 트리를 설명하라. 이때 비율은 얼마인가? 가능한 최소의 비율을 가지는 트리는 어떠한 트리이며, 이 때의 비율은 얼마인가?

최대 비율은 가능한 많은 레드 노드를 가질 때이며, 최대 비율 근사값은 (n-1)/(n+1)이다.

최소 비율은 모든 노드가 블랙 노드로 구성될 때이며, 최소 비율 근사값은 0/n = 0이다.